We’re interested in how slow-feature analysis processes representations generated for a non-Markov task. Towards this end, we apply slow-feature analysis to the hidden layer representation of a recurrent long short-term memory network that solves a non-Markovian task. Importantly, we must first understand the hidden layer representation to see which components to the SFA’d hidden layer representation are generated from the slow-feature process and which were already present in the data.

Raw Hidden Layer and SFA Values

In a previous post, we have the raw hidden layer representation as we loop around the maze. Here is an alternate version of that plot: 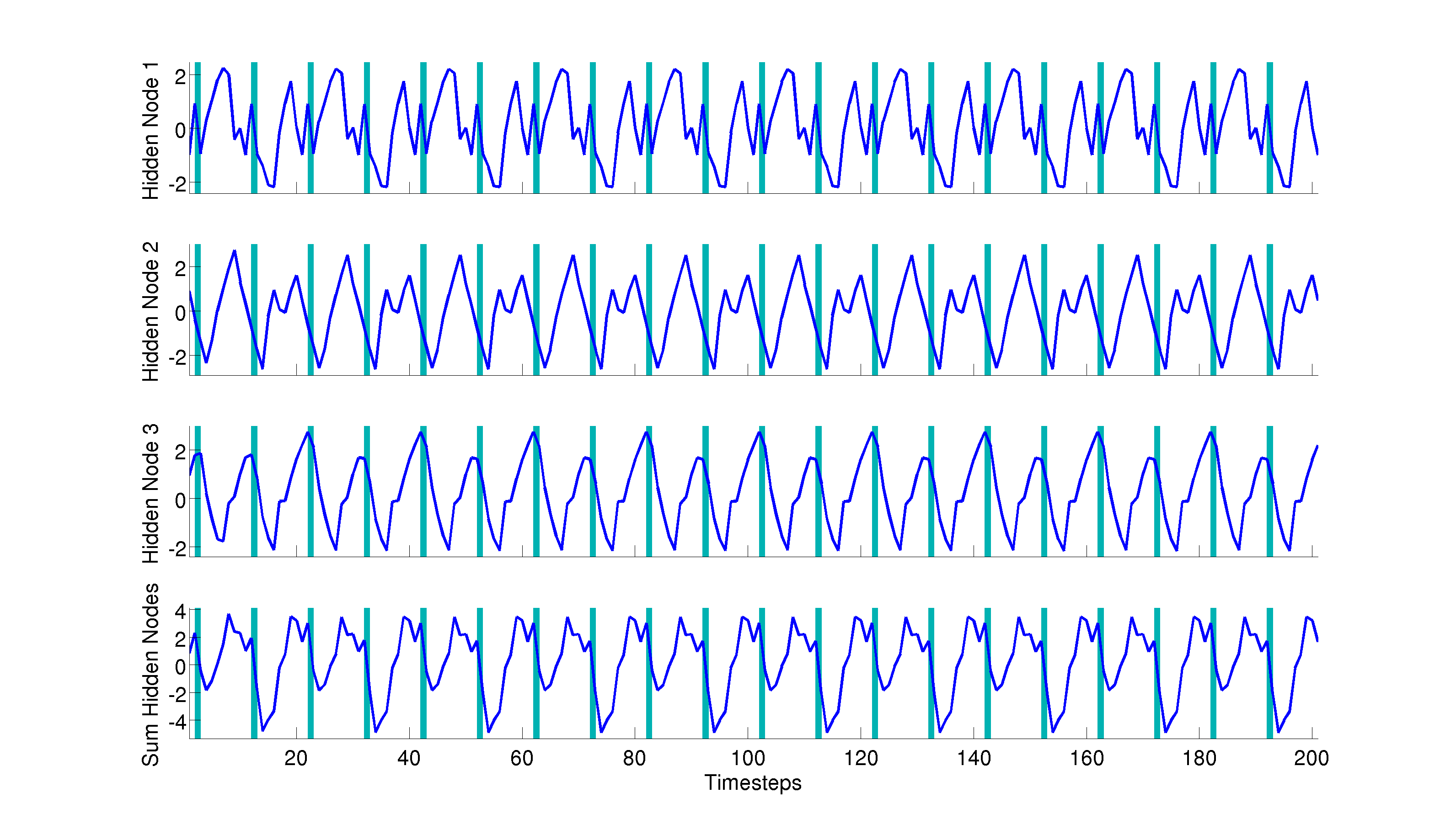Figure 1: The first three subplots show the hidden layer activations for all three hidden nodes. The last subplot shows the sum of all three activations. The blue stripes in the background correspond to the times during which the “rat” is at the fork. Alternating bands correspond to travelling in alternate directions of the maze.

This task is only non-Markovian in the center hallway: the correct action is entirely determined by the current location for all locations on the outside of the maze, but this is not true of the center hallway locations. If we look at hidden node 3, we see that it only differs in value across loop directions at the timepoints near the fork. Essentially, hidden node 3 provides a linearly separable signal that indicates the direction of travel. This is made even clearer in the two plots below showing the hidden layer activations for each location on the maze either on a leftward or rightward loop.

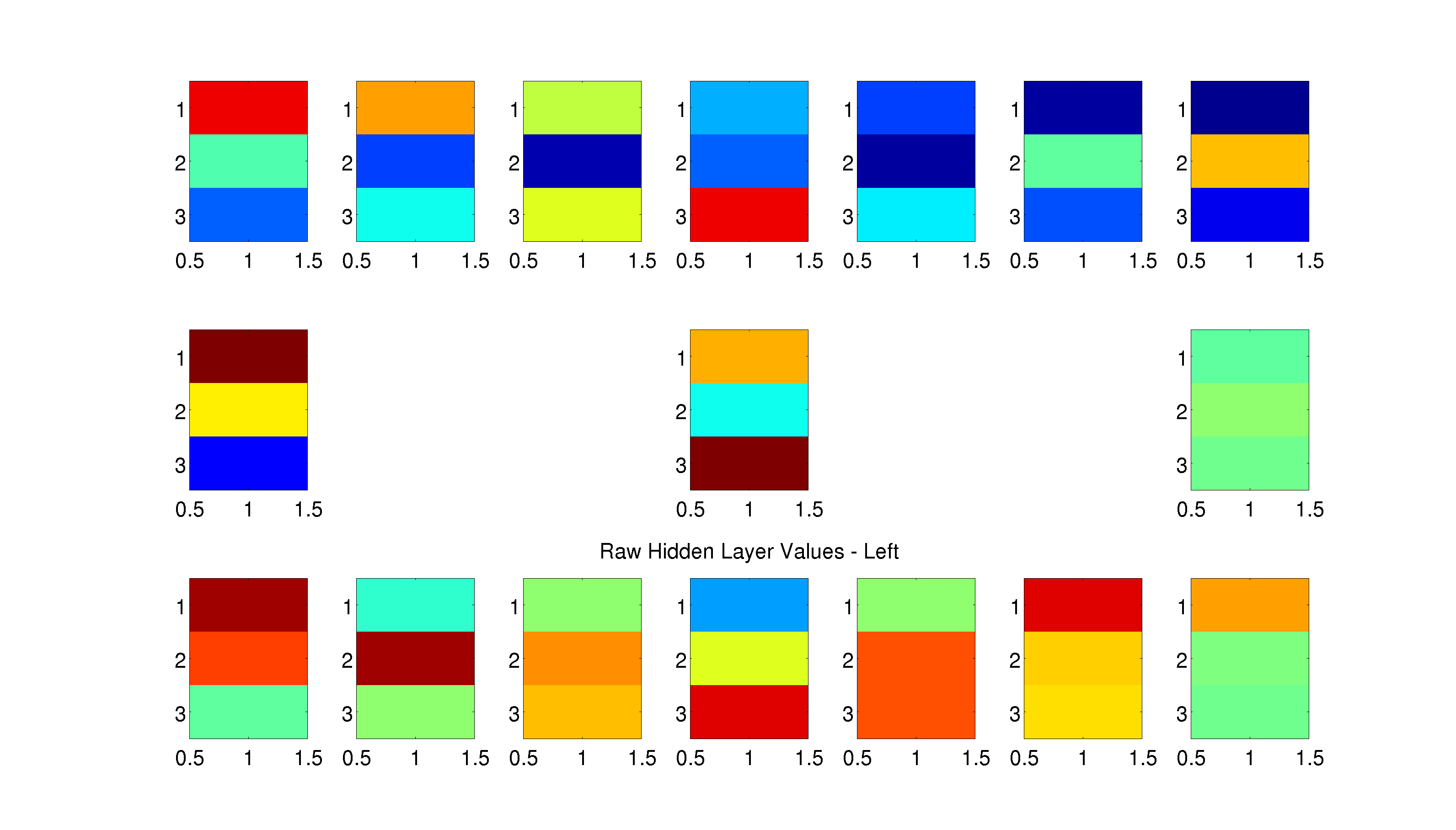
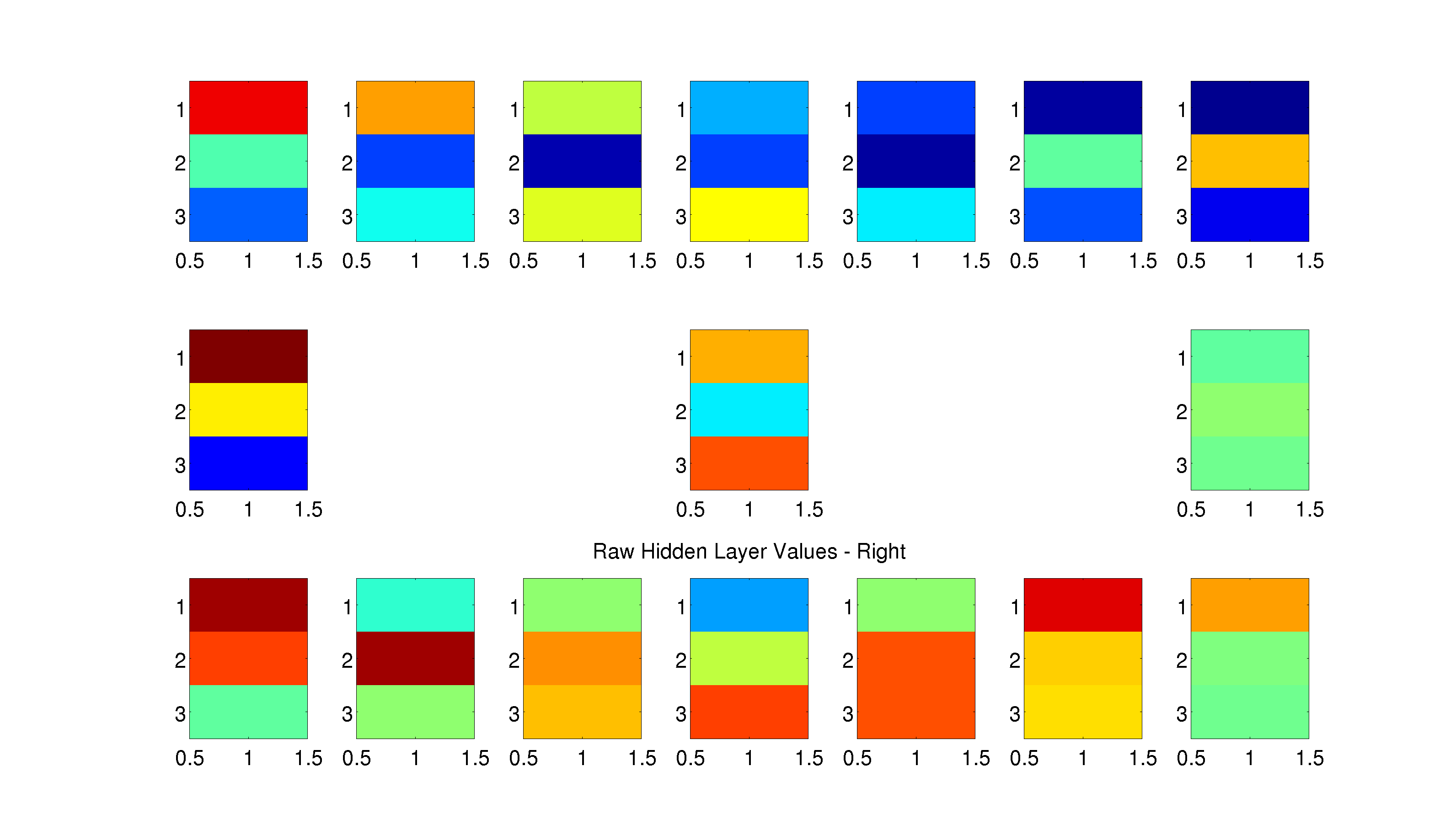
Figure 2: The normalized (-1 to 1) hidden layer representation, a vector of three values: one for each hidden node, for each location in the maze is plotted using imagesc at that location in the maze. This is done for both leftward (top) and rightward (bottom) loops. For example, the subplot in the middle row of the center column on the top plot (“Raw Hidden Layer Values - Left”) shows the hidden layer representation for that location in the maze during a leftward loop. The hidden layer representation for that location during a rightward loop is shown on the bottom plot at the same location. Do not be confused by the fact that the bottom plot for a rightward loop has filled in values for locations on the maze that are only visited during a leftward loop - these are just pasted in from the leftward loop for visualization purposes (and vice-versa for the leftward loop and rightward loop maze locations).

We see that hidden node 3 has different values for the different loops along the center hallway, but nearly symmetric values along the outsides of the maze. It is less clear what the other hidden units may be encoding. A comparison of the first two hidden unit activations across loops shows that they code the outer loops of the maze differently, but not points along the center hallway (Figure 3 below).

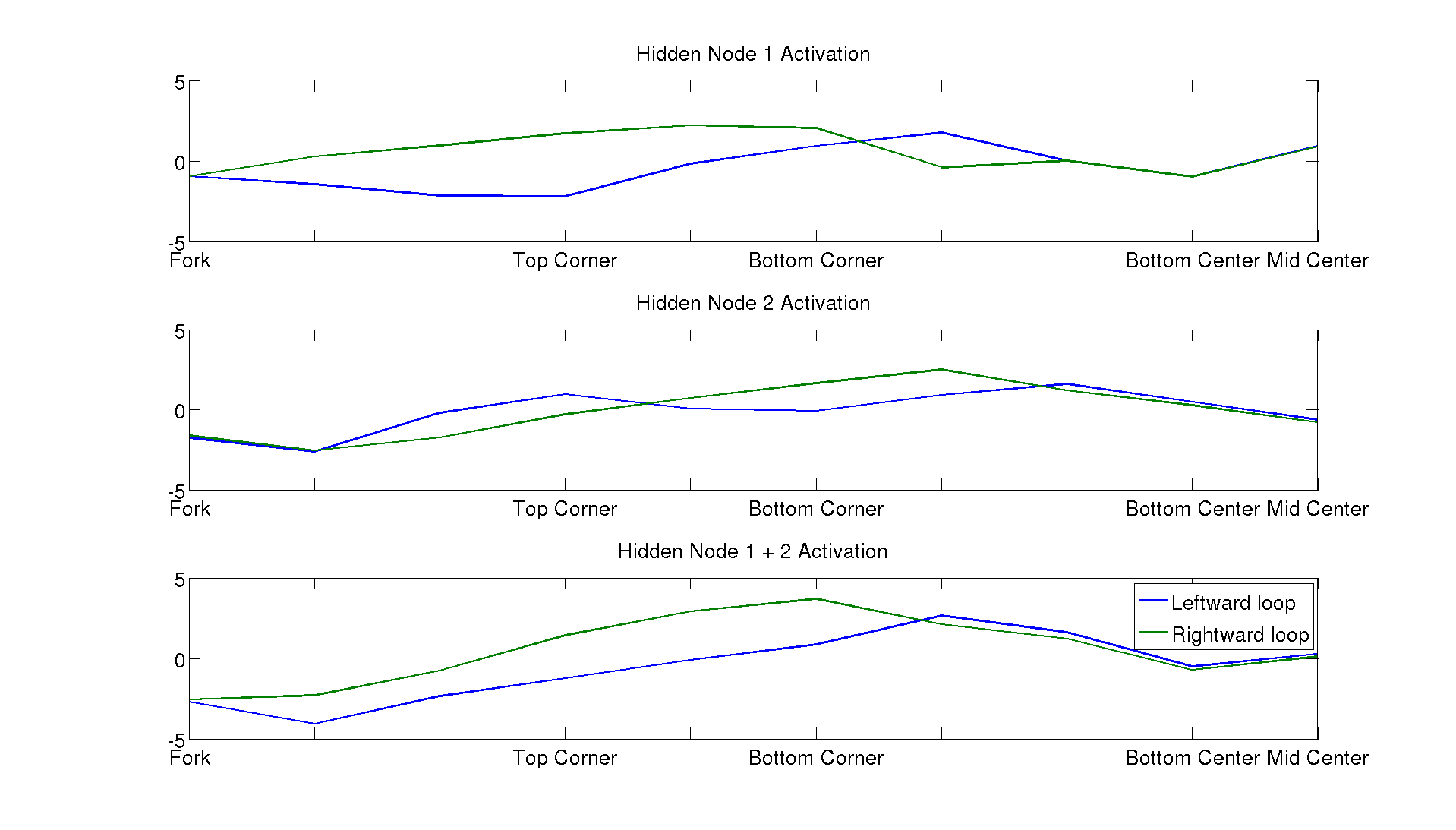Figure 3: Above we plot the activation for the first and second hidden units for each loop direction of the maze and subsequently their sum (bottom plot). The x-axis labels analogous locations in the maze across the loops e.g. “Top Corner” on the middle plot shows the activation of hidden node 2 for the top left corner location (blue) and the the top right corner (green). Notably, the activations are pretty similar for the center hallway locations (“Fork”, “Bottom Center”, and “Mid Center”).

The network does find 20 unique states (the true number of unique states in our task) and we can see this just using the first two hidden unit activations. This begs the question: is the third hidden unit needed? It would be very helpful to plot the multidimensional scaling for all three hidden unit activations, so maybe somebody (cough Luis cough cough a.k.a. my own self cough) should do that here is that plot. Another diagnostic to assess the utility of this third hidden unit would be to look at how the slow-feature analysis output varies based on whether we give all three hidden units or just the first two. 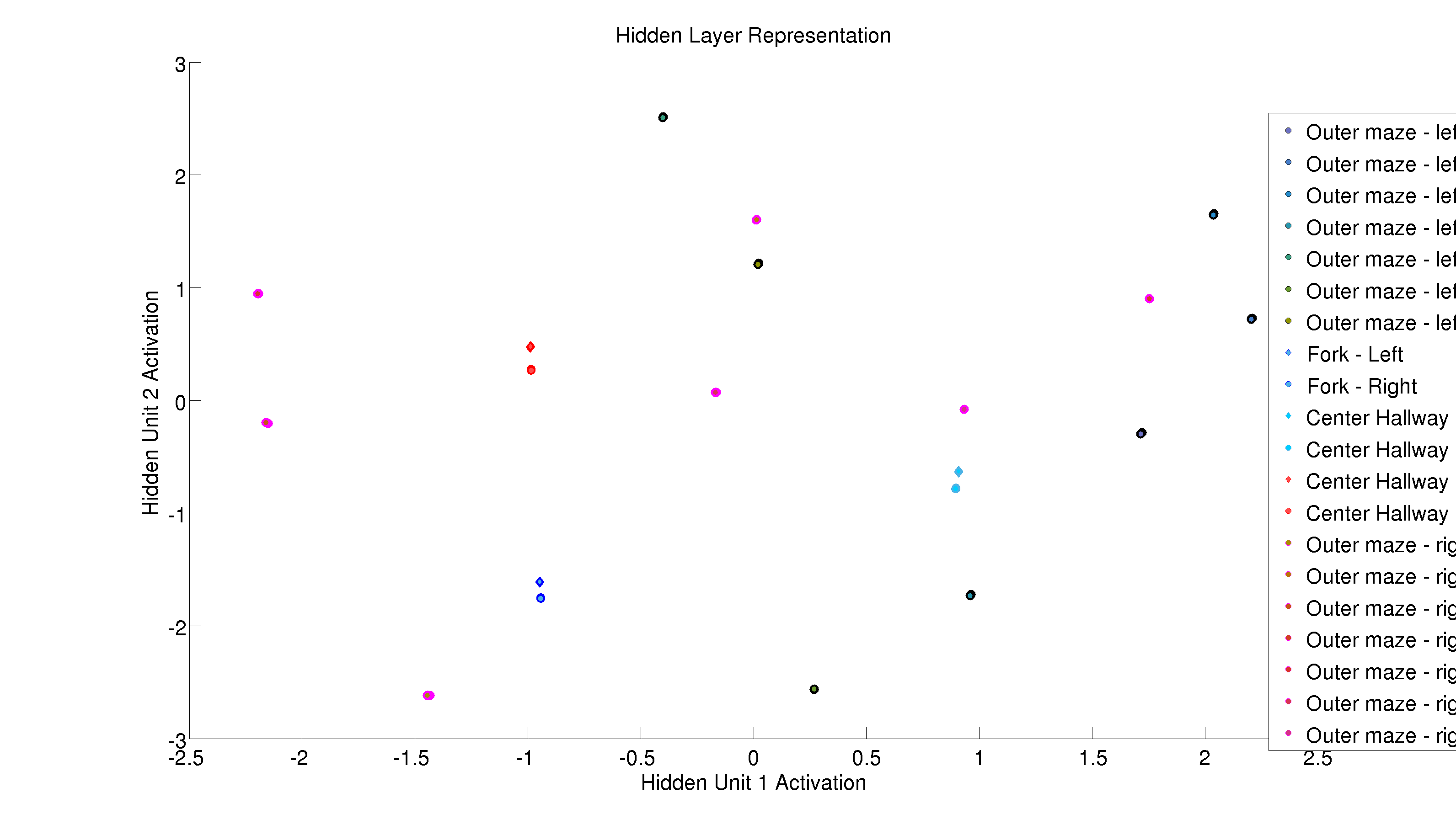Figure 4: Above we plot the hidden unit activations for each time step in our trajectory of 20 loops around the maze. Importantly, locations on the outside of the maze (circles with black or magenta outlines) cluster together across visits. The center locations, however, are cluster according to loop direction.

We can also look at the hidden layer represtation similarity from one location to the other locations as shown below. 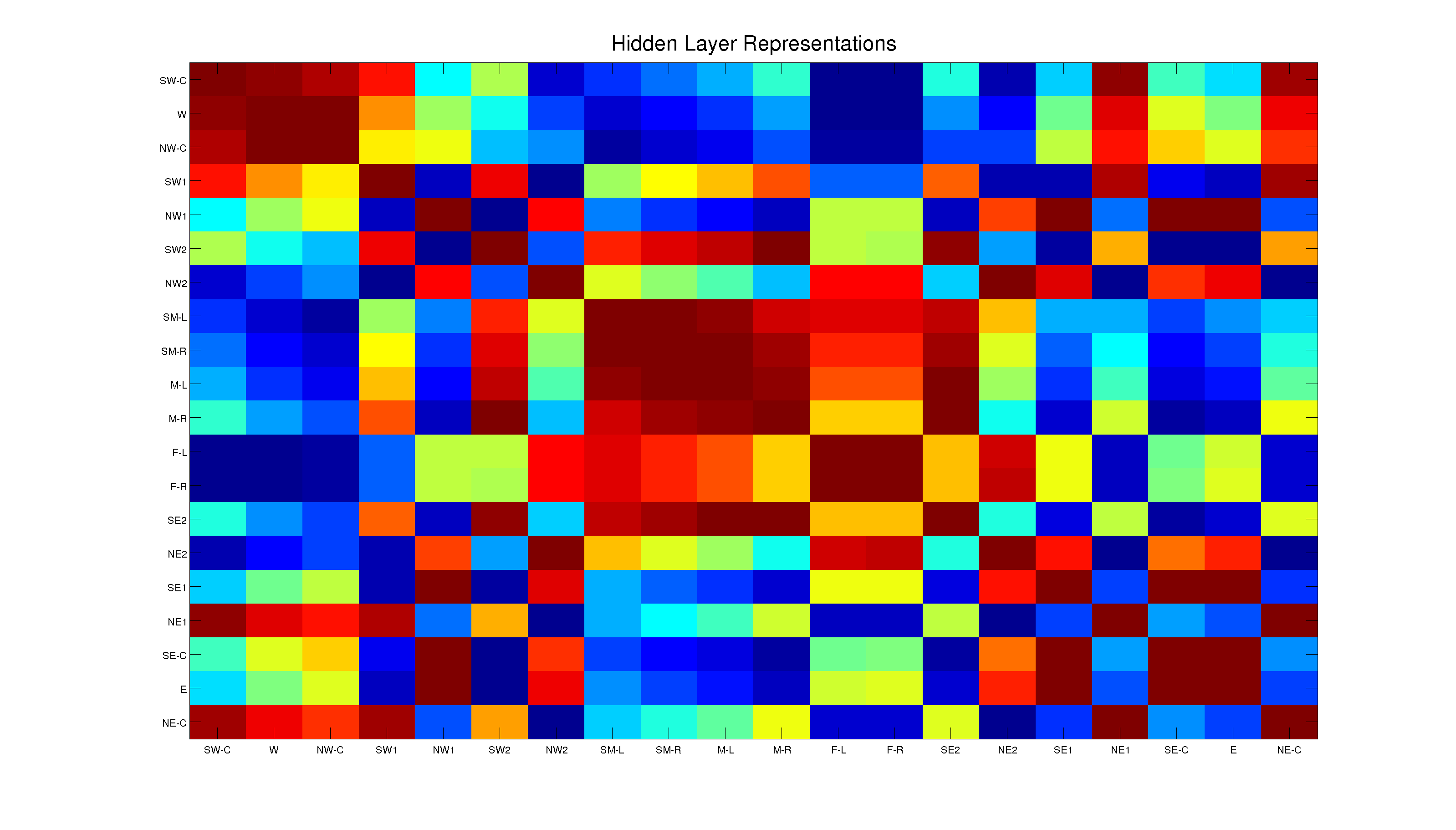Figure 5: This shows the representational similarity for each unique state (recall that not all locations correspond to unique states). The labels along the axes correspond to different locations on the maze (also indicating the loop direction when relevant) using the key below.

Below we show an alternative method for visualizing the hidden layer representation of a location to other locations. 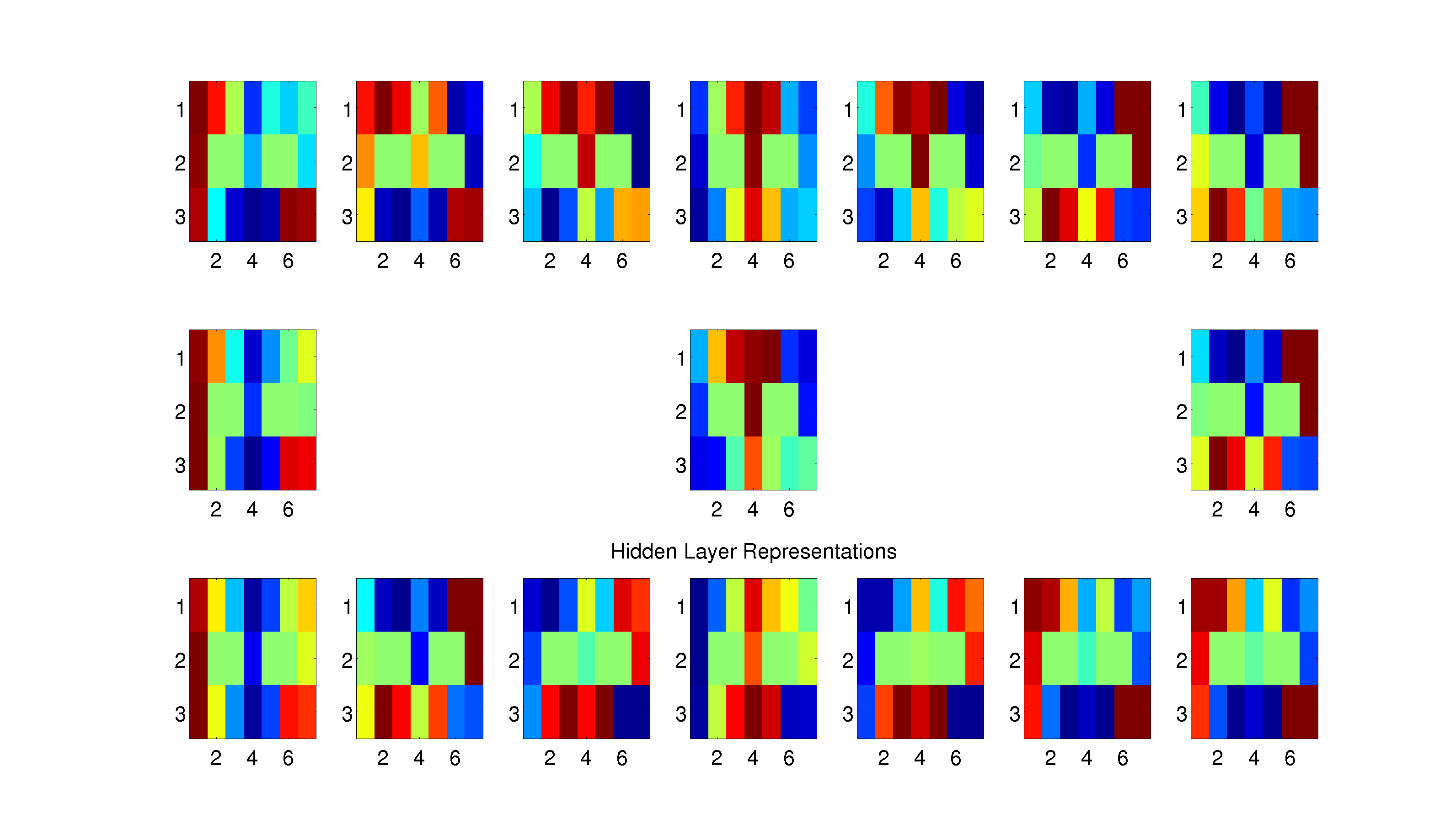Figure 6: For each location in the maze, we create a subplot that shows the hidden layer representation for that location in the maze against all other locations in the maze. For example, to look at the representational similarity between the top-left corner and the bottom-right corner, look at the top-left subplot and the bottom-right square within that subplot. The similarity between a location and itself is also plotted, which is uninformative in the case of locations on the outside of the maze. However, for locations that have multiple states (i.e. the fork location corresponds to both states “Fork - Leftward loop” and “Fork - Rightward loop”), the similarity is plotted across loop directions e.g. the top-center subplot shows the representational similarity for the fork location and the top-center value in that subplot corresponds to the representational similarity between the fork on a leftward loop and the fork on a rightward loop.

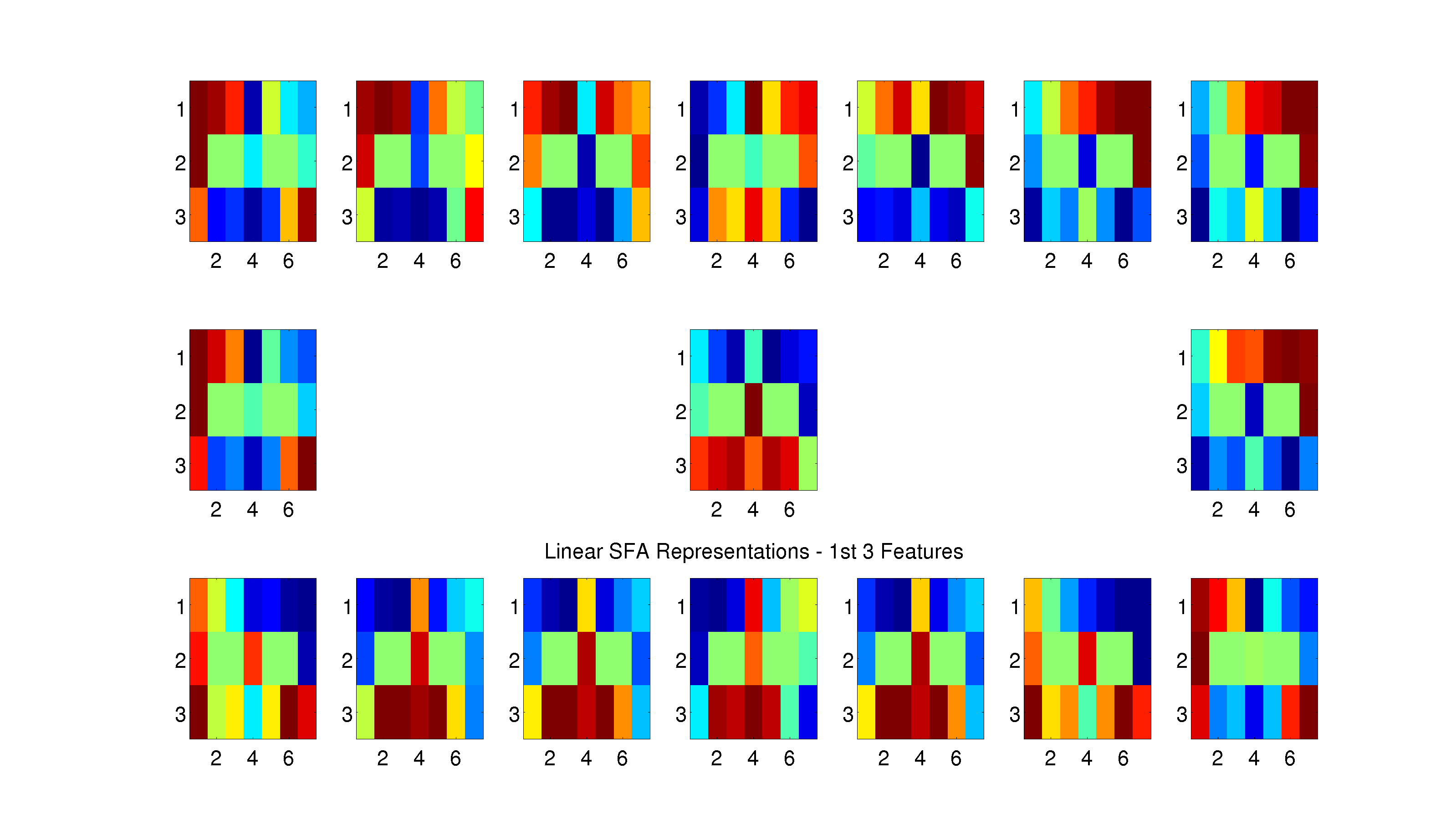
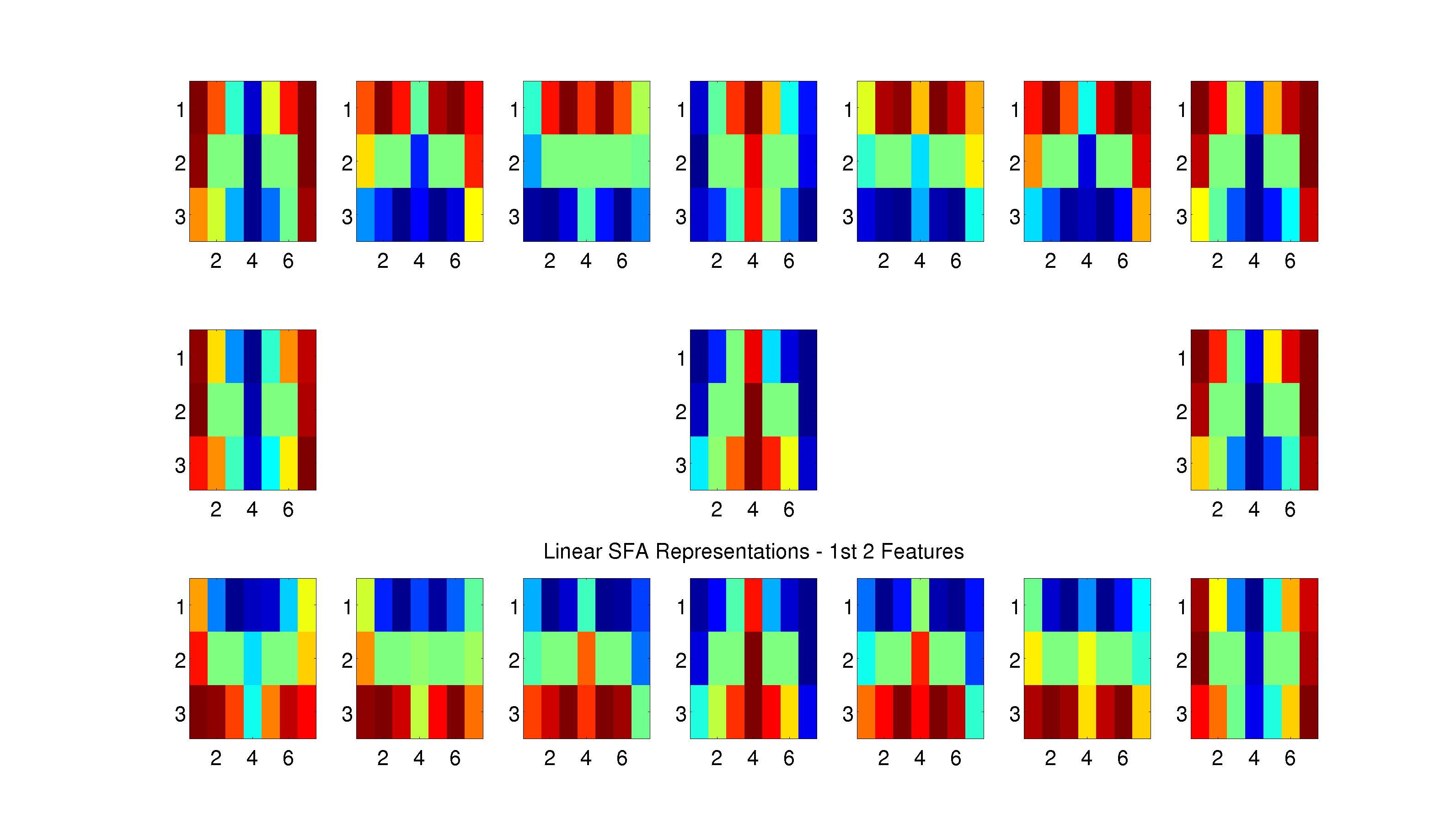
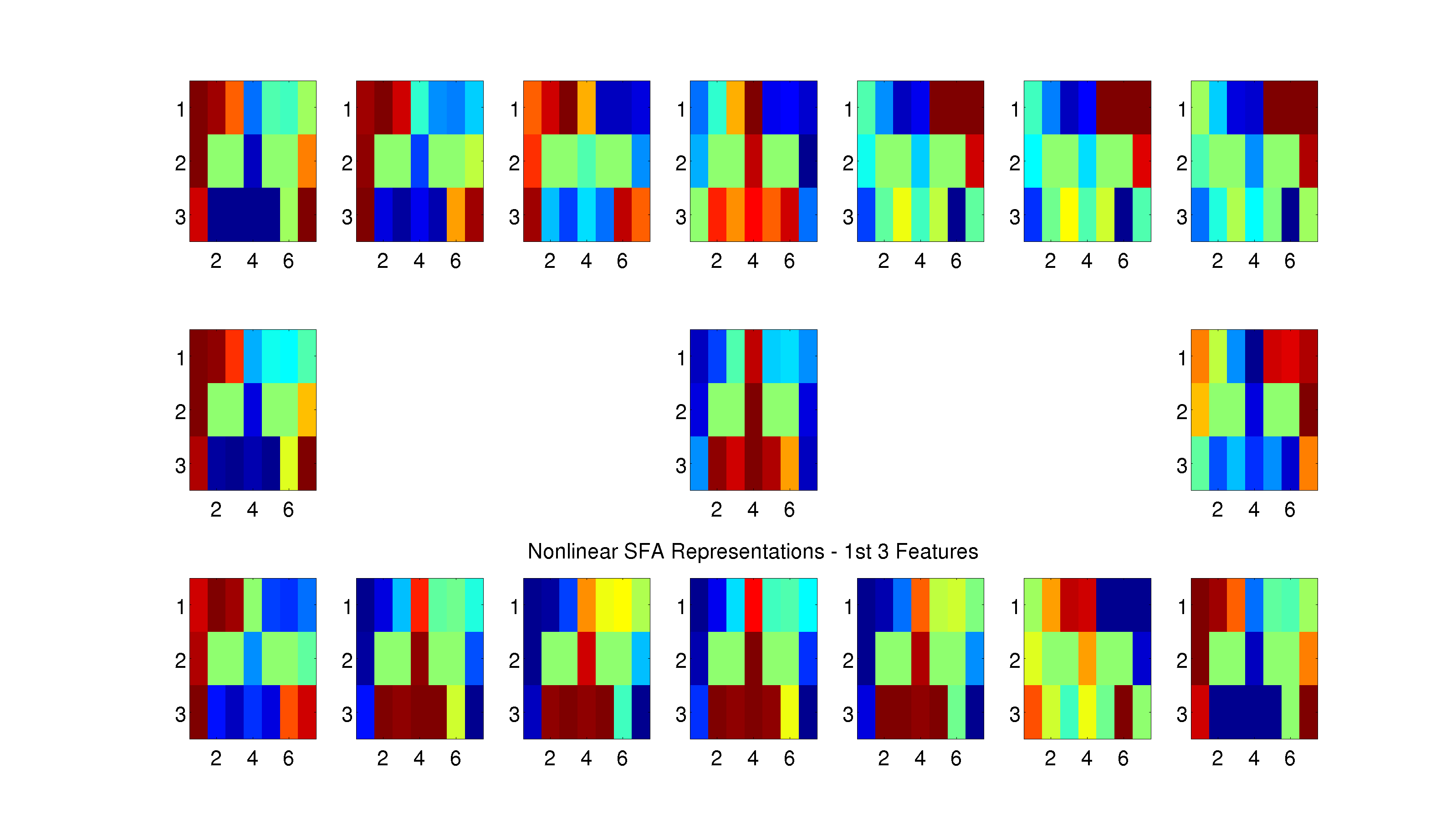
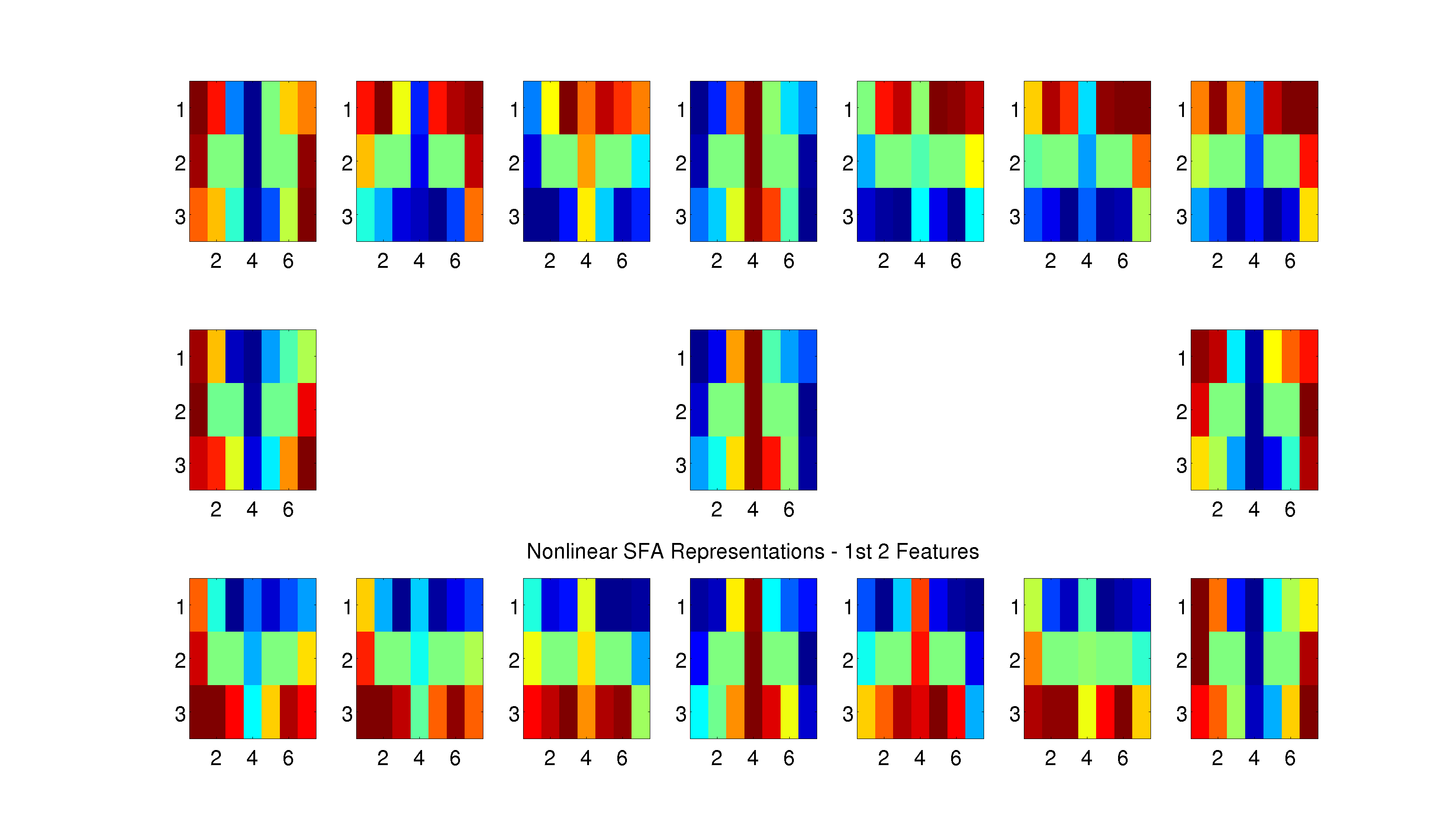
Dump of SFA Similarity Plots